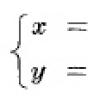Dönen cismin hacmini hesaplayın. Belirli bir integral kullanarak dönel cisimlerin hacimlerinin hesaplanması

12.04.2021

Bir devrim cismin hacmi aşağıdaki formülle hesaplanabilir:

Formülde integralin önünde bir sayı bulunmalıdır. Öyle oldu - hayatta dönen her şey bu sabitle bağlantılıdır.

"A" ve "olmak" entegrasyonunun sınırlarının nasıl belirleneceğini, tamamlanmış çizimden tahmin etmenin kolay olduğunu düşünüyorum.

İşlev... nedir bu işlev? Çizime bakalım. Düz şekil yukarıdan parabol grafiğiyle sınırlanmıştır. Formülde ima edilen fonksiyon budur.

Pratik görevlerde bazen eksenin altına düz bir şekil yerleştirilebilir. Bu hiçbir şeyi değiştirmez - formüldeki fonksiyonun karesi alınır: , dolayısıyla bir devrim cismin hacmi her zaman negatif değildir ki bu oldukça mantıklı.

Bu formülü kullanarak devrim gövdesinin hacmini hesaplayın:

Daha önce de belirttiğim gibi, integral neredeyse her zaman basit çıkıyor, asıl önemli olan dikkatli olmaktır.

Cevap:

Cevapta boyutu - kübik birimleri belirtmek gerekir. Yani dönme gövdemizde yaklaşık 3,35 "küp" vardır. Neden tam olarak kübik birimler? Çünkü en evrensel formülasyon. Santimetreküp olabilir, metreküp olabilir, kilometreküp olabilir vb. Hayal gücünüzün uçan bir daireye kaç tane küçük yeşil adam sığdırabileceği budur.

Örnek 2

Vücudun hacmini bulun rotasyonla oluşturulançizgilerle sınırlanan şeklin ekseni etrafında , ,

Bu kendin yap örneğidir. Dersin sonunda tam çözüm ve cevap.

Pratikte de sıklıkla karşılaşılan iki karmaşık sorunu daha ele alalım.

Örnek 3

, ve çizgileriyle sınırlanan şeklin apsis ekseni etrafında döndürülmesiyle elde edilen cismin hacmini hesaplayın.

Çözüm: Denklemin ekseni tanımladığını unutmadan çizimde , , , çizgileriyle sınırlanmış düz bir şekil gösterelim:

İstenilen şekil mavi renkle gölgelendirilmiştir. Eksen etrafında döndüğünde dört köşeli gerçeküstü bir çörek elde edilir.

Devrim cismin hacmi şu şekilde hesaplanır: vücut hacmi farkı.

Öncelikle kırmızı daire içine alınmış şekle bakalım. Eksen etrafında döndüğünde kesik bir koni elde edilir. Bu kesik koninin hacmini olarak gösterelim.

Yeşil daire içine alınmış şekli düşünün. Bu şekli eksen etrafında döndürürseniz, sadece biraz daha küçük olan kesik bir koni elde edersiniz. Hacmini ile gösterelim.

Ve açıkçası, hacimlerdeki fark tam olarak "çörekimizin" hacmidir.

Dönel bir cismin hacmini bulmak için standart formülü kullanırız:

1) Kırmızıyla daire içine alınmış şekil yukarıdan düz bir çizgiyle sınırlanmıştır, bu nedenle:

2) Yeşil daire içine alınmış şekil yukarıdan düz bir çizgiyle sınırlanmıştır, bu nedenle:

3) İstenilen devir gövdesinin hacmi:

Cevap:

Bu durumda çözümün kesik koninin hacmini hesaplamak için okul formülü kullanılarak kontrol edilebilmesi ilginçtir.

Kararın kendisi genellikle daha kısa yapılır, şöyle bir şey:

Şimdi biraz ara verelim ve geometrik illüzyonlardan bahsedelim.

İnsanlar genellikle Perelman'ın (aynı değil) kitapta fark ettiği ciltlerle ilgili yanılsamalar yaşarlar. İlginç geometri. Çözülmüş problemdeki düz şekle bakın - alan olarak küçük görünüyor ve devrimin gövdesinin hacmi 50 kübik birimin biraz üzerinde, bu da çok büyük görünüyor. Bu arada, ortalama bir insan tüm hayatı boyunca 18 metrekarelik bir oda hacmine sahip bir sıvı içer, bu da tam tersine çok küçük bir hacim gibi görünüyor.

Genel olarak SSCB'deki eğitim sistemi gerçekten en iyisiydi. Perelman'ın 1950'de yazdığı aynı kitap, mizahçının dediği gibi, akıl yürütmeyi çok iyi geliştiriyor ve size sorunlara orijinal standart dışı çözümler aramayı öğretiyor. Son zamanlarda bazı bölümleri büyük bir ilgiyle yeniden okudum, tavsiye ediyorum, insani yardımseverlerin bile erişebileceği bir kitap. Hayır, spontovy eğlencenin, bilgeliğin ve iletişimde geniş bir bakış açısının harika bir şey olduğunu önerdiğimde gülümsemenize gerek yok.

Lirik bir incelemeden sonra, yaratıcı bir görevi çözmek tam olarak uygundur:

Örnek 4

Çizgilerle sınırlanan düz bir şeklin ekseni etrafında döndürülmesiyle oluşan bir cismin hacmini hesaplayın.

Bu kendin yap örneğidir. Bantta her şeyin gerçekleştiğini, yani neredeyse hazır entegrasyon limitlerinin verildiğini unutmayın. Ayrıca, eğer argüman ikiye bölünürse, trigonometrik fonksiyonların grafiklerini doğru bir şekilde çizmeye çalışın: , grafikler eksen boyunca iki kez uzatılır. En az 3-4 puan bulmaya çalışın trigonometrik tablolara göre ve çizimi daha doğru hale getirin. Dersin sonunda tam çözüm ve cevap. Bu arada, görev çok rasyonel değil, rasyonel olarak çözülebilir.

Dönmeyle oluşan bir cismin hacminin hesaplanması
bir eksen etrafında düz şekil

İkinci paragraf birincisinden daha da ilginç olacak. Y ekseni etrafında dönen bir cismin hacmini hesaplama görevi de testlerde oldukça sık karşılaşılan bir görevdir. Geçerken dikkate alınacak bir şeklin alanını bulma problemi ikinci yol - eksen boyunca entegrasyon, bu yalnızca becerilerinizi geliştirmenize olanak sağlamakla kalmayacak, aynı zamanda size en karlı çözümü nasıl bulacağınızı da öğretecektir. Aynı zamanda pratik bir anlamı da var! Matematik öğretim yöntemleri öğretmenimin gülümseyerek hatırladığı gibi, birçok mezun ona şu sözlerle teşekkür etti: “Konunuzun bize çok faydası oldu, artık etkili yöneticileriz ve personelimizi en iyi şekilde yönetiyoruz.” Bu fırsatı değerlendirerek, özellikle edinilen bilgiyi amacına uygun olarak kullandığım için ona da büyük şükranlarımı sunuyorum =).

Örnek 5

Çizgilerle sınırlanmış düz bir şekil verildiğinde , , .

1) Bu çizgilerle sınırlanan düz bir şeklin alanını bulun.
2) Bu çizgilerle sınırlanan düz bir şeklin eksen etrafında döndürülmesiyle elde edilen cismin hacmini bulun.

Dikkat! Sadece ikinci paragrafı okumak isteseniz bile, önce mutlaka ilkini oku!

Çözüm: Görev iki bölümden oluşuyor. Kareyle başlayalım.

1) Çizimi gerçekleştirelim:

Fonksiyonun parabolün üst dalını, fonksiyonun da parabolün alt dalını tanımladığını görmek kolaydır. Önümüzde "kendi tarafında duran" önemsiz bir parabol var.

Alanı bulunacak olan istenilen şekil mavi renkle gölgelendirilmiştir.

Bir şeklin alanı nasıl bulunur? Derste ele alınan "olağan" şekilde bulunabilir. Kesin integral. Bir şeklin alanı nasıl hesaplanır. Ayrıca şeklin alanı alanların toplamı olarak bulunur:
- segmentte;
- segmentte.

Bu yüzden:

Bu durumda olağan çözümde yanlış olan ne? Öncelikle iki integral var. İkincisi, integrallerin altındaki kökler ve integrallerin kökleri bir hediye değildir, üstelik integralin sınırlarını değiştirirken kafa karışabilir. Aslında integraller elbette ölümcül değil, ancak pratikte her şey çok daha üzücü, görev için sadece "daha iyi" işlevler seçtim.

Daha rasyonel bir çözüm var: Ters fonksiyonlara geçiş ve eksen boyunca entegrasyondan ibarettir.

Ters fonksiyonlara nasıl geçilir? Kabaca söylemek gerekirse, "x"i "y"ye kadar ifade etmeniz gerekir. İlk önce parabolle ilgilenelim:

Bu kadarı yeterli ama aynı fonksiyonun alt daldan da türetilebildiğinden emin olalım:

Düz bir çizgiyle her şey daha kolaydır:

Şimdi eksene bakın: lütfen açıklarken başınızı periyodik olarak 90 derece sağa doğru eğin (bu bir şaka değil!). İhtiyacımız olan rakam kırmızı noktalı çizgiyle gösterilen segmentin üzerinde yer alıyor. Aynı zamanda, segmentte düz bir çizgi parabolün üzerinde bulunur; bu, şeklin alanının size zaten tanıdık gelen formül kullanılarak bulunması gerektiği anlamına gelir:. Formülde neler değişti? Sadece bir mektup, başka bir şey değil.

! Not: Eksen boyunca entegrasyon sınırları belirlenmelidir kesinlikle aşağıdan yukarıya!

Alanı bulmak:

Bu nedenle segmentte:

Entegrasyonu nasıl gerçekleştirdiğime dikkat edin, bu en rasyonel yoldur ve ödevin bir sonraki paragrafında bunun nedeni açıklanacaktır.

Entegrasyonun doğruluğundan şüphe duyan okuyucular için türevleri bulacağım:

Orijinal integrand elde edilir, bu da integrasyonun doğru yapıldığı anlamına gelir.

Cevap:

2) Bu şeklin eksen etrafında dönmesiyle oluşan cismin hacmini hesaplayınız.

Çizimi biraz farklı bir tasarımla yeniden çizeceğim:

Yani mavi renkle gölgelenen şekil eksen etrafında dönmektedir. Sonuç, kendi ekseni etrafında dönen bir "havada uçan kelebek"tir.

Dönel cismin hacmini bulmak için eksen boyunca integral alacağız. Öncelikle ters fonksiyonlara geçmemiz gerekiyor. Bu zaten önceki paragrafta ayrıntılı olarak yapılmış ve açıklanmıştır.

Şimdi başımızı tekrar sağa eğip figürümüzü inceliyoruz. Açıkçası, devrim gövdesinin hacmi, hacimler arasındaki fark olarak bulunmalıdır.

Kırmızı daire içine alınmış şekli eksen etrafında döndürerek kesik bir koni elde ederiz. Bu hacmi ile gösterelim.

Yeşil daire içine alınmış şekli eksen etrafında döndürüyoruz ve ortaya çıkan devrim gövdesinin hacmiyle belirtiyoruz.

Kelebeğimizin hacmi hacim farkına eşittir.

Dönel bir cismin hacmini bulmak için formülü kullanırız:

Önceki paragrafın formülünden farkı nedir? Sadece harflerle.

Ve işte burada az önce bahsettiğim integralin avantajı, önce integrandın 4. kuvvetine ulaşmaktan çok daha kolay.

Cevap:

Ancak hasta bir kelebek.

Aynı düz şeklin eksen etrafında döndürülmesi durumunda, doğal olarak farklı bir hacimde tamamen farklı bir devrim gövdesinin ortaya çıkacağını unutmayın.

Örnek 6

Çizgilerle sınırlanmış düz bir şekil ve bir eksen verilmiştir.

1) Ters fonksiyonlara gidin ve değişken üzerinden integral alarak bu çizgilerle sınırlanan düz bir şeklin alanını bulun.
2) Bu çizgilerle sınırlanan düz bir şeklin eksen etrafında döndürülmesiyle elde edilen cismin hacmini hesaplayınız.

Bu kendin yap örneğidir. Dileyenler şeklin alanını da "olağan" şekilde bulabilir, böylece 1. maddedeki testi tamamlayabilirler. Ancak tekrar ediyorum, düz bir şekli eksen etrafında döndürürseniz, o zaman farklı bir hacme sahip tamamen farklı bir dönme gövdesi elde edersiniz, bu arada, doğru cevap (ayrıca çözmeyi sevenler için).

Dersin sonunda görevin önerilen iki öğesinin tam çözümü.

Ayrıca rotasyon gövdelerini ve entegrasyon kapsamını anlamak için başınızı sağa eğmeyi unutmayın!

Zaten makaleyi bitirmek istiyordum ama bugün sadece y ekseni etrafındaki bir devrimin hacmini bulmak için ilginç bir örnek getirdiler. Taze:

Örnek 7

ve eğrileriyle sınırlanan şeklin ekseni etrafında dönmesiyle oluşan cismin hacmini hesaplayınız. Parabolün kullanılmayan sol dalı ters fonksiyona karşılık gelir - fonksiyonun grafiği eksenin üzerindeki segmentte bulunur;

Bir devrim cismi hacminin, zaten devrim cisimlerinin hacimlerinin toplamı olarak aranması gerektiğini varsaymak mantıklıdır!

Formülü kullanıyoruz:

Bu durumda:

Cevap:

İÇİNDE bir şeklin alanını bulma problemi alanların toplamı sıklıkla kullanılır ve devrim cisimlerinin hacimlerinin toplamı görünüşe göre nadirdir, çünkü böyle bir çeşitlilik neredeyse görüş alanımın dışına çıkmıştır. Yine de, ele alınan örneğin zamanında ortaya çıkması iyi bir şey - birçok yararlı şeyi çıkarmayı başardık.

Rakamların başarılı tanıtımı!

Bir devrim cismin hacmi formülle hesaplanabilir:

Formülde integralin önünde bir sayı bulunmalıdır. Öyle oldu - hayatta dönen her şey bu sabitle bağlantılıdır.

"A" ve "olmak" entegrasyonunun sınırlarının nasıl belirleneceğini, tamamlanmış çizimden tahmin etmenin kolay olduğunu düşünüyorum.

İşlev... nedir bu işlev? Çizime bakalım. Düz şekil üstteki parabolik grafikle sınırlanmıştır. Formülde ima edilen fonksiyon budur.

Pratik görevlerde bazen eksenin altına düz bir şekil yerleştirilebilir. Bu hiçbir şeyi değiştirmez - formüldeki integralin karesi alınır: dolayısıyla integral her zaman negatif değildir ki bu oldukça mantıklı.

Bu formülü kullanarak devrim gövdesinin hacmini hesaplayın:

Daha önce de belirttiğim gibi, integral neredeyse her zaman basit çıkıyor, asıl önemli olan dikkatli olmaktır.

Cevap:

Cevapta boyutu - kübik birimleri belirtmek gerekir. Yani dönme gövdemizde yaklaşık 3,35 "küp" vardır. Neden tam olarak kübik birimler? Çünkü en evrensel formülasyon. Santimetreküp olabilir, metreküp olabilir, kilometreküp olabilir vb., hayal gücünüzün uçan bir daireye kaç tane küçük yeşil adam sığdırabileceği budur.

Örnek 2

Çizgilerle sınırlanan şeklin ekseni etrafında döndürülmesiyle oluşan cismin hacmini bulun,

Bu kendin yap örneğidir. Dersin sonunda tam çözüm ve cevap.

Pratikte de sıklıkla karşılaşılan iki karmaşık sorunu daha ele alalım.

Örnek 3

Çizgilerle sınırlanan şeklin apsis ekseni etrafında döndürülmesiyle elde edilen cismin hacmini hesaplayın ve

Çözüm: Çizimde denklemin ekseni belirlediğini unutmadan çizgilerle çevrelenmiş düz bir şekil çizelim:

İstenilen şekil mavi renkle gölgelendirilmiştir. Eksen etrafında döndüğünde dört köşeli gerçeküstü bir çörek elde edilir.

Devrim cismin hacmi şu şekilde hesaplanır: vücut hacmi farkı.

Öncelikle kırmızı daire içine alınmış şekle bakalım. Eksen etrafında döndüğünde kesik bir koni elde edilir. Bu kesik koninin hacmini ile belirtin.

Yeşil daire içine alınmış şekli düşünün. Bu şekli eksen etrafında döndürürseniz, sadece biraz daha küçük olan kesik bir koni elde edersiniz. Hacmini ile gösterelim.

Ve açıkçası, hacimlerdeki fark tam olarak "çörekimizin" hacmidir.

Dönel bir cismin hacmini bulmak için standart formülü kullanırız:

1) Kırmızıyla daire içine alınmış şekil yukarıdan düz bir çizgiyle sınırlanmıştır, bu nedenle:

2) Yeşil daire içine alınmış şekil yukarıdan düz bir çizgiyle sınırlanmıştır, bu nedenle:

3) İstenilen devir gövdesinin hacmi:

Cevap:

Bu durumda çözümün kesik koninin hacmini hesaplamak için okul formülü kullanılarak kontrol edilebilmesi ilginçtir.

Kararın kendisi genellikle daha kısa yapılır, şöyle bir şey:

Şimdi biraz ara verelim ve geometrik illüzyonlardan bahsedelim.

İnsanlar genellikle ciltlerle ilgili yanılsamalar yaşarlar; Perelman (başka biri) bunu kitapta fark etmiştir. İlginç geometri. Çözülmüş problemdeki düz şekle bakın - alan olarak küçük görünüyor ve devrimin gövdesinin hacmi 50 kübik birimin biraz üzerinde, bu da çok büyük görünüyor. Bu arada, hayatı boyunca ortalama bir insan, 18 metrekarelik bir oda hacmine sahip bir sıvıyı içiyor, bu da tam tersine çok küçük bir hacim gibi görünüyor.

Genel olarak SSCB'deki eğitim sistemi gerçekten en iyisiydi. Perelman'ın 1950'de yayınlanan aynı kitabı, mizahçının dediği gibi, akıl yürütmeyi çok iyi geliştiriyor ve size sorunlara orijinal standart dışı çözümler aramayı öğretiyor. Son zamanlarda bazı bölümleri büyük bir ilgiyle yeniden okudum, tavsiye ediyorum, insani yardımseverlerin bile erişebileceği bir kitap. Hayır, spontovy eğlencenin, bilgeliğin ve iletişimde geniş bir bakış açısının harika bir şey olduğunu önerdiğimde gülümsemenize gerek yok.

Lirik bir incelemeden sonra, yaratıcı bir görevi çözmek tam olarak uygundur:

Örnek 4

Çizgilerle sınırlanan bir düzlemsel şeklin ekseni etrafında dönmesiyle oluşan cismin hacmini hesaplayınız.

Bu kendin yap örneğidir. Unutmayın ki her şey bantta gerçekleşir, yani aslında hazır entegrasyon limitleri verilmiştir. Trigonometrik fonksiyonların grafiklerini doğru çizin, size dersin materyalini hatırlatacağım grafiklerin geometrik dönüşümleri : eğer argüman ikiye bölünebilirse: , grafikler eksen boyunca iki kez uzatılır. En az 3-4 puan bulunması arzu edilir trigonometrik tablolara göre çizimi daha doğru bir şekilde tamamlamak için. Dersin sonunda tam çözüm ve cevap. Bu arada, görev çok rasyonel değil, rasyonel olarak çözülebilir.

Hat sınırlı olsun. Düzlem şekli kutupsal koordinat sisteminde verilmiştir.

Örnek: Çevreyi hesaplayın: x 2 +y 2 =R 2

I çeyreğinde yer alan dairenin 4. kısmının uzunluğunu hesaplayın (х≥0, y≥0):

Eğrinin denklemi param-th formunda verilirse:
x(t), y(t) fonksiyonları tanımlıdır ve türevleriyle birlikte [α,β] aralığında süreklidir. Türev, daha sonra formülde bir değişiklik yaparak:
ve buna göre

aldık
çarpan ekle
kök işaretinin altında ve sonunda elde ediyoruz

Not: Bir düzlemsel eğri verilmiştir, uzaydaki parametrelerle verilen bir fonksiyonu da düşünebilirsiniz, ardından z=z(t) fonksiyonu eklenecek ve formül

Örnek: Aşağıdaki denklemle verilen asteroitin uzunluğunu hesaplayın: x=a*cos 3 (t), y=a*sin 3 (t), a>0

4. parçanın uzunluğunu hesaplayın:

formüle göre

Kutupsal koordinat sisteminde verilen bir düzlem eğrinin yayının uzunluğu:

Eğrinin denklemi kutupsal koordinat sisteminde verilsin:
[α,β] segmentindeki türeviyle birlikte sürekli bir fonksiyondur.

Kutupsal koordinatlardan geçiş formülleri:

parametrik olarak kabul edilir:

ϕ - parametre, f-le'ye göre

Örn: Eğri uzunluğunu hesaplayın:
>0

Z-tion: çevrenin yarısını hesaplayın:

Vücudun kesit alanından hesaplanan bir vücudun hacmi.

Kapalı bir yüzeyle sınırlanmış bir cisim verilsin ve bu cismin herhangi bir bölümünün alanı Ox eksenine dik bir düzlemle bilinsin. Bu alan kesme düzleminin konumuna bağlı olacaktır.

tüm cismin x eksenine dik olan ve x=a, x=b (a) noktalarında kesişen 2 düzlem arasında çevrelenmesine izin verin.

Böyle bir cismin hacmini belirlemek için, Ox eksenine dik ve noktalarda kesişen kesen düzlemleri kullanarak onu katmanlara böleriz. Her kısmi aralıkta
. Haydi seçelim

ve her i=1,….,n değeri için, generatrisi Ox'a paralel olan silindirik bir gövde inşa ediyoruz ve kılavuz, gövdenin kesitinin x=С i düzlemine göre konturu, hacmi taban alanı S=C i ve yüksekliği ∆х i olan böyle bir temel silindir. V ben =S(C i)∆x ben . Bu tür temel silindirlerin hepsinin hacmi
. Bu toplamın limiti, eğer varsa ve maksimum ∆х  0'da sonlu ise, verilen cismin hacmi denir.

. Vn, parça üzerinde sürekli S(x) fonksiyonunun integral toplamı olduğundan, belirtilen limit mevcuttur (varlığın t-ma'sı) ve def ile ifade edilir. integral.

- kesit alanından hesaplanan vücut hacmi.

Devrimin gövdesinin hacmi:

Cismin, y=f(x) fonksiyonunun grafiği, Öküz ekseni ve x=a, x=b düz çizgileriyle sınırlanan eğrisel bir yamuğun Öküz ekseni etrafında döndürülmesiyle oluşturulmuş olsun.

y=f(x) fonksiyonunun doğru parçası üzerinde tanımlı ve sürekli olmasına ve üzerinde negatif olmamasına izin verin, o zaman bu cismin Ox'a dik bir düzlemle kesiti yarıçapı R=y(x)=f(x) olan bir dairedir. ). S (x) \u003d Py 2 (x) \u003d P 2 dairesinin alanı. Formülün değiştirilmesi
Öküz ekseni etrafında dönen bir cismin hacmini hesaplamak için bir formül elde ederiz:

Bununla birlikte, eğrisel bir yamuk, fonksiyon üzerinde sürekli bir grafikle sınırlanan Oy ekseni etrafında dönüyorsa, o zaman böyle bir devrim cismin hacmi:

Aynı hacim aşağıdaki formül kullanılarak hesaplanabilir:
. Doğru parametrik denklemlerle verilmişse:

Değişkeni değiştirerek şunu elde ederiz:

Doğru parametrik denklemlerle verilmişse:

y (α)= c , y (β)= d . y = y (t) değişikliğini yaparak şunu elde ederiz:

Parabolün y ekseni etrafındaki devrim cisimlerini hesaplayın, .

2) Düz bir çizgi y \u003d 0, bir yay ile sınırlanan eğrisel bir yamuğun OX ekseni etrafındaki devir gövdesinin V'sini hesaplayın (merkez (1;0) noktasında ve yarıçap=1) ile .

Bir devrim cismin yüzey alanı

Verilen yüzeyin y=f(x) eğrisinin x ekseni etrafında döndürülmesiyle oluştuğunu varsayalım. Bu yüzeyin S'sini belirlemek gereklidir.

Y \u003d f (x) fonksiyonunun belirli ve sürekli olmasına izin verin, [a; c] segmentinin tüm noktalarında negatif ve negatif olsun

Uzunluklarını sırasıyla belirttiğimiz akorları çizelim (n-akorlar)

Lagrange teoremine göre:

Sınırlandırılmış kesik çizginin tamamının yüzey alanı şuna eşit olacaktır:

Tanım: Bu toplamın limiti, eğer sonlu ise, çoklu çizginin en büyük bağlantısı olduğunda max , dikkate alınan devrim yüzeyinin alanı olarak adlandırılır.

Toplamın yüz limitinin, p-th için entegre toplamın limitine eşit olduğu kanıtlanabilir.

Dönel bir cismin S yüzeyi için formül =

x=g(x) eğrisinin yayının Oy ekseni etrafında dönmesiyle oluşan yüzeyin S'si

Türevi ile sürekli

Eğri parametrik olarak ur-mi ile verilirseX=x(t) ,sen= T(T) işlevlerX’(T), sen’(T), X(T), sen(T) aralıkta tanımlanır [A; B], X(A)= A, X(B)= Bdaha sonra oyuncu değişikliğini yapıyoruzX= X(T)

Eğri parametrik olarak verilirse formülde değişiklik yapılırsa şunu elde ederiz:

Eğrinin denklemi kutupsal koordinat sisteminde verilirse

Seksen etrafında dönme yüzeyi şuna eşit olacaktır:

Alanı bulma probleminde olduğu gibi, kendinize güvenen çizim becerilerine ihtiyacınız var - bu neredeyse en önemli şeydir (çünkü integrallerin kendileri genellikle kolay olacaktır). Metodolojik materyallerin ve grafiklerin geometrik dönüşümlerinin yardımıyla yetkin ve hızlı bir grafik tekniğine hakim olabilirsiniz. Ama aslında derste çizimlerin öneminden defalarca bahsettim.

Genel olarak, integral hesabında pek çok ilginç uygulama vardır; belirli bir integralin yardımıyla bir şeklin alanını, bir devrim cismin hacmini, yay uzunluğunu, yüzey alanını hesaplayabilirsiniz. rotasyon ve çok daha fazlası. Bu yüzden eğlenceli olacak, lütfen iyimser olun!

Koordinat düzleminde düz bir şekil hayal edin. Temsil edildi mi? ... Kimin neyi sunduğunu merak ediyorum ... =))) Alanını zaten bulduk. Ancak ek olarak, bu şekil iki şekilde de döndürülebilir ve döndürülebilir:

- apsis ekseni etrafında;
- y ekseni etrafında.

Bu yazıda her iki durum da ele alınacaktır. İkinci döndürme yöntemi özellikle ilginçtir, en büyük zorluklara neden olur, ancak aslında çözüm, x ekseni etrafında daha yaygın olan döndürmeyle hemen hemen aynıdır. Bonus olarak geri döneceğim bir şeklin alanını bulma problemi ve alanı ikinci şekilde - eksen boyunca - nasıl bulacağınızı anlatacağım. Malzemenin temaya çok iyi uyması bir bonus bile değil.

En popüler rotasyon türüyle başlayalım.

bir eksen etrafında düz şekil

örnek 1

Çizgilerle sınırlanan şeklin eksen etrafında döndürülmesiyle elde edilen cismin hacmini hesaplayın.

Çözüm: Alan probleminde olduğu gibi, çözüm düz bir şekil çizmekle başlar. Yani, düzlemde denklemin ekseni tanımladığını unutmadan çizgilerle sınırlanmış bir şekil oluşturmak gerekir. Bir çizimin nasıl daha rasyonel ve daha hızlı hale getirileceğini sayfalarda bulabilirsiniz. Temel Fonksiyonların Grafikleri ve Özellikleri Ve Kesin integral. Bir şeklin alanı nasıl hesaplanır. Bu bir Çin hatırlatmasıdır ve bu noktada durmuyorum.

Buradaki çizim oldukça basit:

İstenilen düz şekil mavi renkle gölgelendirilmiş olup, eksen etrafında dönen bu şekildir.Dönme sonucunda eksene göre simetrik olan hafif yumurta şeklinde bir uçan daire elde edilir. Aslında vücudun matematiksel bir adı var ama referans kitabında bir şeyi belirtmek çok tembel, o yüzden devam ediyoruz.

Bir devrim cismin hacmi nasıl hesaplanır?

Bir devrim cismin hacmi formülle hesaplanabilir:

Formülde integralin önünde bir sayı bulunmalıdır. Öyle oldu - hayatta dönen her şey bu sabitle bağlantılıdır.

"A" ve "olmak" entegrasyonunun sınırlarının nasıl belirleneceğini, tamamlanmış çizimden tahmin etmenin kolay olduğunu düşünüyorum.

İşlev... nedir bu işlev? Çizime bakalım. Düz şekil yukarıdan parabol grafiğiyle sınırlanmıştır. Formülde ima edilen fonksiyon budur.

Pratik görevlerde bazen eksenin altına düz bir şekil yerleştirilebilir. Bu hiçbir şeyi değiştirmez - formüldeki integralin karesi alınır: , dolayısıyla integral her zaman negatif değildir ki bu oldukça mantıklı.

Bu formülü kullanarak devrim gövdesinin hacmini hesaplayın:

Daha önce de belirttiğim gibi, integral neredeyse her zaman basit çıkıyor, asıl önemli olan dikkatli olmaktır.

Cevap:

Örnek 2

, , çizgileriyle sınırlanan şeklin ekseni etrafında döndürülmesiyle oluşan cismin hacmini bulun.

Bu kendin yap örneğidir. Dersin sonunda tam çözüm ve cevap.

Pratikte de sıklıkla karşılaşılan iki karmaşık sorunu daha ele alalım.

Örnek 3

, ve çizgileriyle sınırlanan şeklin apsis ekseni etrafında döndürülmesiyle elde edilen cismin hacmini hesaplayın.

Çözüm: Çizimde , , , çizgileriyle sınırlanmış düz bir şekil çizin, ancak denklemin ekseni tanımladığını unutmayın:

İstenilen şekil mavi renkle gölgelendirilmiştir. Eksen etrafında döndüğünde dört köşeli gerçeküstü bir çörek elde edilir.

Devrim cismin hacmi şu şekilde hesaplanır: vücut hacmi farkı.

Öncelikle kırmızı daire içine alınmış şekle bakalım. Eksen etrafında döndüğünde kesik bir koni elde edilir. Bu kesik koninin hacmini olarak gösterelim.

Yeşil daire içine alınmış şekli düşünün. Bu şekli eksen etrafında döndürürseniz, sadece biraz daha küçük olan kesik bir koni elde edersiniz. Hacmini ile gösterelim.

Ve açıkçası, hacimlerdeki fark tam olarak "çörekimizin" hacmidir.

Dönel bir cismin hacmini bulmak için standart formülü kullanırız:

1) Kırmızıyla daire içine alınmış şekil yukarıdan düz bir çizgiyle sınırlanmıştır, bu nedenle:

2) Yeşil daire içine alınmış şekil yukarıdan düz bir çizgiyle sınırlanmıştır, bu nedenle:

3) İstenilen devir gövdesinin hacmi:

Cevap:

Bu durumda çözümün kesik koninin hacmini hesaplamak için okul formülü kullanılarak kontrol edilebilmesi ilginçtir.

Kararın kendisi genellikle daha kısa yapılır, şöyle bir şey:

Şimdi biraz ara verelim ve geometrik illüzyonlardan bahsedelim.

İnsanlar genellikle ciltlerle ilgili yanılsamalar yaşarlar; Perelman (başka biri) bunu kitapta fark etmiştir. İlginç geometri. Çözülmüş problemdeki düz şekle bakın - alan olarak küçük görünüyor ve devrimin gövdesinin hacmi 50 kübik birimin biraz üzerinde, bu da çok büyük görünüyor. Bu arada, ortalama bir insan tüm hayatı boyunca 18 metrekarelik bir oda hacmine sahip bir sıvı içer, bu da tam tersine çok küçük bir hacim gibi görünüyor.

Lirik bir incelemeden sonra, yaratıcı bir görevi çözmek tam olarak uygundur:

Örnek 4

Çizgilerle sınırlanan düz bir şeklin ekseni etrafında döndürülmesiyle oluşan bir cismin hacmini hesaplayın.

Bu kendin yap örneğidir. Unutmayın ki her şey bantta gerçekleşir, yani aslında hazır entegrasyon limitleri verilmiştir. Trigonometrik fonksiyonların grafiklerini doğru çizin, size dersin materyalini hatırlatacağım grafiklerin geometrik dönüşümleri: eğer argüman ikiye bölünebilirse: , grafikler eksen boyunca iki kez uzatılır. En az 3-4 puan bulunması arzu edilir trigonometrik tablolara göreçizimi daha doğru bir şekilde tamamlamak için. Dersin sonunda tam çözüm ve cevap. Bu arada, görev çok rasyonel değil, rasyonel olarak çözülebilir.

Dönmeyle oluşan bir cismin hacminin hesaplanması
bir eksen etrafında düz şekil

Herkesin okumasını, hatta kuklaları tamamlamasını tavsiye ederim. Ayrıca, ikinci paragrafın özetlenen materyali çift katlı integrallerin hesaplanmasında paha biçilemez bir yardım sağlayacaktır..

Örnek 5

Çizgilerle sınırlanmış düz bir şekil verildiğinde , , .

1) Bu çizgilerle sınırlanan düz bir şeklin alanını bulun.
2) Bu çizgilerle sınırlanan düz bir şeklin eksen etrafında döndürülmesiyle elde edilen cismin hacmini bulun.

Dikkat! Sadece ikinci paragrafı okumak isteseniz bile, önce mutlaka ilkini oku!

Çözüm: Görev iki bölümden oluşmaktadır. Kareyle başlayalım.

1) Çizimi gerçekleştirelim:

Fonksiyonun parabolün üst dalını, fonksiyonun da parabolün alt dalını tanımladığını görmek kolaydır. Önümüzde "kendi tarafında duran" önemsiz bir parabol var.

Alanı bulunacak olan istenilen şekil mavi renkle gölgelendirilmiştir.

Bu yüzden:

Daha rasyonel bir çözüm var: Ters fonksiyonlara geçiş ve eksen boyunca entegrasyondan ibarettir.

Ters fonksiyonlara nasıl geçilir? Kabaca söylemek gerekirse, "x"i "y"ye kadar ifade etmeniz gerekir. İlk önce parabolle ilgilenelim:

Bu kadarı yeterli ama aynı fonksiyonun alt daldan da türetilebildiğinden emin olalım:

Düz bir çizgiyle her şey daha kolaydır:

Şimdi eksene bakın: lütfen açıklarken başınızı periyodik olarak 90 derece sağa doğru eğin (bu bir şaka değil!). İhtiyacımız olan rakam kırmızı noktalı çizgiyle gösterilen segmentin üzerinde yer alıyor. Dahası, segmentte düz bir çizgi parabolün üzerinde bulunur; bu, şeklin alanının size zaten tanıdık gelen formül kullanılarak bulunması gerektiği anlamına gelir: . Formülde neler değişti? Sadece bir mektup, başka bir şey değil.

! Not: Eksen boyunca entegrasyon sınırları ayarlanmalıdır kesinlikle aşağıdan yukarıya!

Alanı bulmak:

Bu nedenle segmentte:

Entegrasyonu nasıl gerçekleştirdiğime dikkat edin, bu en rasyonel yoldur ve ödevin bir sonraki paragrafında bunun nedeni açıklanacaktır.

Entegrasyonun doğruluğundan şüphe duyan okuyucular için türevleri bulacağım:

Orijinal integrand elde edilir, bu da integrasyonun doğru yapıldığı anlamına gelir.

Cevap:

2) Bu şeklin eksen etrafında dönmesiyle oluşan cismin hacmini hesaplayınız.

Çizimi biraz farklı bir tasarımla yeniden çizeceğim:

Yani mavi renkle gölgelenen şekil eksen etrafında dönmektedir. Sonuç, kendi ekseni etrafında dönen bir "havada uçan kelebek"tir.

Şimdi başımızı tekrar sağa eğip figürümüzü inceliyoruz. Açıkçası, devrim gövdesinin hacmi, hacimler arasındaki fark olarak bulunmalıdır.

Kırmızı daire içine alınmış şekli eksen etrafında döndürerek kesik bir koni elde ederiz. Bu hacmi ile gösterelim.

Yeşil daire içine alınmış şekli eksen etrafında döndürüyoruz ve ortaya çıkan devrim gövdesinin hacmiyle belirtiyoruz.

Kelebeğimizin hacmi hacim farkına eşittir.

Dönel bir cismin hacmini bulmak için formülü kullanırız:

Önceki paragrafın formülünden farkı nedir? Sadece harflerle.

Ve işte yakın zamanda bahsettiğim entegrasyonun avantajını bulmak çok daha kolay İntegrali 4'üncü kuvvete yükseltmektense.

Cevap:

Ancak hasta bir kelebek.

Aynı düz şeklin eksen etrafında döndürülmesi durumunda, doğal olarak farklı bir hacimde tamamen farklı bir devrim gövdesinin ortaya çıkacağını unutmayın.

Örnek 6

Çizgilerle sınırlanmış düz bir şekil ve bir eksen verilmiştir.

Dersin sonunda görevin önerilen iki öğesinin tam çözümü.

Ayrıca rotasyon gövdelerini ve entegrasyon kapsamını anlamak için başınızı sağa eğmeyi unutmayın!

Benzer makaleler: