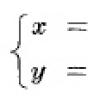Vypočítajte objem rotačného telesa. Výpočet objemov rotačných telies pomocou určitého integrálu

Objem rotačného telesa možno vypočítať podľa vzorca:

Vo vzorci musí byť pred integrálom číslo. Stalo sa to - všetko, čo sa v živote točí, je spojené s touto konštantou.

Ako nastaviť hranice integrácie "a" a "byť", myslím, je ľahké uhádnuť z dokončeného výkresu.

Funkcia... čo je táto funkcia? Pozrime sa na výkres. Plochý obrazec je zhora ohraničený grafom paraboly. Toto je funkcia, ktorá je zahrnutá vo vzorci.

V praktických úlohách môže byť plochá postava niekedy umiestnená pod osou. To nič nemení - funkcia vo vzorci je odmocnená: , teda objem rotačného telesa je vždy nezáporný, čo je celkom logické.

Vypočítajte objem rotačného telesa pomocou tohto vzorca:

Ako som už poznamenal, integrál sa takmer vždy ukáže ako jednoduchý, hlavnou vecou je byť opatrný.

odpoveď:

V odpovedi je potrebné uviesť rozmer - kubické jednotky. To znamená, že v našom rotačnom tele je približne 3,35 "kociek". Prečo práve kubický Jednotky? Pretože najuniverzálnejšia formulácia. Môžu tam byť kubické centimetre, môžu tam byť kubické metre, môžu byť kubické kilometre atď., toľko malých zelených mužíkov sa vo vašej fantázii zmestí do lietajúceho taniera.

Príklad 2

Nájdite objem tela tvorené rotáciou okolo osi obrazca ohraničeného čiarami , ,

Toto je príklad „urob si sám“. Úplné riešenie a odpoveď na konci hodiny.

Uvažujme o dvoch zložitejších problémoch, s ktorými sa v praxi tiež často stretávame.

Príklad 3

Vypočítajte objem telesa získaného rotáciou okolo osi x úsečky obrazca ohraničeného priamkami , , a

Riešenie: Znázornime na výkrese plochý obrazec ohraničený čiarami , , , , pričom nezabúdajme, že rovnica definuje os:

Požadovaná figúrka je vytieňovaná modrou farbou. Keď sa otáča okolo osi, získa sa taká neskutočná šiška so štyrmi rohmi.

Objem rotačného telesa sa vypočíta ako rozdiel v objeme tela.

Najprv sa pozrime na postavu, ktorá je zakrúžkovaná červenou farbou. Keď sa otáča okolo osi, získa sa zrezaný kužeľ. Označme objem tohto zrezaného kužeľa ako .

Zvážte postavu, ktorá je zakrúžkovaná zelenou farbou. Ak otočíte tento obrazec okolo osi, získate tiež zrezaný kužeľ, len o niečo menší. Jeho objem označme .

A samozrejme, rozdiel v objemoch je presne objemom našej „šišky“.

Na zistenie objemu rotačného telesa používame štandardný vzorec:

1) Číslo zakrúžkované červenou farbou je zhora ohraničené priamkou, preto:

2) Obrázok zakrúžkovaný zelenou farbou je zhora ohraničený priamkou, preto:

3) Objem požadovaného rotačného telesa:

odpoveď:

Je zvláštne, že v tomto prípade je možné riešenie skontrolovať pomocou školského vzorca na výpočet objemu zrezaného kužeľa.

Samotné rozhodnutie sa často robí kratšie, asi takto:

Teraz si dáme prestávku a povieme si niečo o geometrických ilúziách.

Ľudia majú často ilúzie spojené so zväzkami, čo si Perelman (nie ten istý) v knihe všimol Zaujímavá geometria. Pozrite sa na plochý obrázok v riešenom probléme - zdá sa, že je malý na plochu a objem rotačného telesa je len niečo málo cez 50 kubických jednotiek, čo sa zdá byť príliš veľké. Mimochodom, priemerný človek za celý život vypije tekutinu s objemom miestnosti 18 metrov štvorcových, čo sa mu naopak zdá príliš malý objem.

Vo všeobecnosti bol vzdelávací systém v ZSSR skutočne najlepší. Tá istá kniha od Perelmana, ktorú napísal ešte v roku 1950, sa veľmi dobre rozvíja, ako povedal humorista, uvažovaním a učí vás hľadať originálne neštandardné riešenia problémov. Nedávno som si s veľkým záujmom znovu prečítal niektoré kapitoly, odporúčam, je to prístupné aj pre humanistov. Nie, nemusíte sa usmievať, že som navrhol bespontovu zábavu, erudícia a široký rozhľad v komunikácii sú super vec.

Po lyrickej odbočke je vhodné vyriešiť kreatívnu úlohu:

Príklad 4

Vypočítajte objem telesa vytvoreného rotáciou okolo osi plochého útvaru ohraničeného priamkami , , kde .

Toto je príklad „urob si sám“. Upozorňujeme, že všetky veci sa dejú v pásme, inými slovami, sú dané takmer hotové integračné limity. Pokúste sa tiež správne nakresliť grafy goniometrických funkcií, ak je argument rozdelený dvoma: , potom sa grafy roztiahnu pozdĺž osi dvakrát. Pokúste sa nájsť aspoň 3-4 body podľa trigonometrických tabuliek a spresniť kresbu. Úplné riešenie a odpoveď na konci hodiny. Mimochodom, úloha sa dá vyriešiť racionálne a nie veľmi racionálne.

Výpočet objemu telesa vzniknutého rotáciou
plochá postava okolo osi

Druhý odsek bude ešte zaujímavejší ako prvý. Úloha vypočítať objem rotačného telesa okolo osi y je tiež pomerne častým návštevníkom testov. Priebežne sa bude brať do úvahy problém nájsť oblasť postavy druhý spôsob - integrácia pozdĺž osi, to vám umožní nielen zlepšiť svoje zručnosti, ale tiež vás naučí, ako nájsť najziskovejšie riešenie. Má to aj praktický význam! Ako s úsmevom spomínala moja učiteľka metód vyučovania matematiky, mnohí absolventi jej ďakovali slovami: „Váš predmet nám veľmi pomohol, teraz sme efektívni manažéri a svojich zamestnancov riadime optimálne.“ Využívajúc túto príležitosť, vyjadrujem jej tiež veľkú vďaku, najmä preto, že získané vedomosti využívam na zamýšľaný účel =).

Príklad 5

Daný plochý obrazec ohraničený čiarami , , .

1) Nájdite plochu plochej postavy ohraničenú týmito čiarami.
2) Nájdite objem telesa získaný otočením plochého útvaru ohraničeného týmito čiarami okolo osi.

Pozor! Aj keď si chcete najskôr prečítať len druhý odsek Nevyhnutne prečítajte si prvý!

Riešenie:Úloha pozostáva z dvoch častí. Začnime námestím.

1) Vykonajte kreslenie:

Je ľahké vidieť, že funkcia definuje hornú vetvu paraboly a funkcia definuje dolnú vetvu paraboly. Pred nami je triviálna parabola, ktorá „leží na boku“.

Požadovaná postava, ktorej oblasť sa má nájsť, je zatienená modrou farbou.

Ako nájsť oblasť postavy? Dá sa nájsť „zvyčajným“ spôsobom, o ktorom sa uvažovalo v lekcii. Určitý integrál. Ako vypočítať plochu obrázku. Okrem toho sa oblasť obrázku nachádza ako súčet oblastí:
- na segmente;
- na segmente.

Preto:

Čo je v tomto prípade zlé na zvyčajnom riešení? Po prvé, existujú dva integrály. Po druhé, odmocniny pod integrálmi a odmocniny v integráloch nie sú darom, navyše sa človek môže zmiasť pri nahrádzaní hraníc integrácie. V skutočnosti integrály, samozrejme, nie sú smrteľné, ale v praxi je všetko oveľa smutnejšie, len som pre túto úlohu vybral „lepšie“ funkcie.

Existuje racionálnejšie riešenie: spočíva v prechode na inverzné funkcie a integrácii pozdĺž osi.

Ako prejsť na inverzné funkcie? Zhruba povedané, musíte vyjadriť "x" cez "y". Najprv sa pozrime na parabolu:

To stačí, ale presvedčte sa, že rovnakú funkciu možno odvodiť aj zo spodnej vetvy:

S priamou čiarou je všetko jednoduchšie:

Teraz sa pozrite na os: pravidelne nakláňajte hlavu doprava o 90 stupňov, ako vysvetľujete (toto nie je vtip!). Obrázok, ktorý potrebujeme, leží na segmente, ktorý je označený červenou bodkovanou čiarou. Zároveň je na segmente priamka umiestnená nad parabolou, čo znamená, že oblasť obrázku by sa mala nájsť pomocou vzorca, ktorý už poznáte:. Čo sa zmenilo vo vzorci? Iba list a nič viac.

! Poznámka: Mali by sa nastaviť limity integrácie pozdĺž osi striktne zdola nahor!

Nájdenie oblasti:

V segmente teda:

Venujte pozornosť tomu, ako som vykonal integráciu, je to najracionálnejší spôsob a v ďalšom odseku zadania bude jasné prečo.

Pre čitateľov, ktorí pochybujú o správnosti integrácie, nájdem deriváty:

Získa sa pôvodný integrand, čo znamená, že integrácia je vykonaná správne.

odpoveď:

2) Vypočítajte objem telesa, ktoré vznikne rotáciou tohto obrazca okolo osi.

Výkres prekreslím do trochu iného dizajnu:

Postava vytieňovaná modrou sa teda otáča okolo osi. Výsledkom je „vznášajúci sa motýľ“, ktorý sa otáča okolo svojej osi.

Aby sme našli objem rotačného telesa, budeme integrovať pozdĺž osi. Najprv musíme prejsť k inverzným funkciám. Toto už bolo urobené a podrobne popísané v predchádzajúcom odseku.

Teraz opäť nakloníme hlavu doprava a študujeme našu postavu. Je zrejmé, že objem rotačného telesa by sa mal nájsť ako rozdiel medzi objemami.

Otáčame figúrku zakrúžkovanú červenou farbou okolo osi, výsledkom čoho je zrezaný kužeľ. Označme tento zväzok .

Zeleným zakrúžkovaným obrazcom otáčame okolo osi a označujeme ho cez objem výsledného rotačného telesa.

Objem nášho motýľa sa rovná rozdielu v objemoch.

Na zistenie objemu rotačného telesa používame vzorec:

Ako sa líši od vzorca z predchádzajúceho odseku? Iba v listoch.

A tu je výhoda integrácie, o ktorej som nedávno hovoril, je oveľa ľahšie nájsť, ako najprv zvýšiť integrand na 4. mocninu.

odpoveď:

Avšak chorľavý motýľ.

Všimnite si, že ak sa rovnaká plochá postava otáča okolo osi, potom sa ukáže úplne iné rotačné telo s iným, prirodzene, objemom.

Príklad 6

Daný plochý obrazec ohraničený čiarami a osou.

1) Prejdite na inverzné funkcie a nájdite oblasť plochej postavy ohraničenú týmito čiarami integráciou cez premennú .
2) Vypočítajte objem telesa získaného otáčaním plochého útvaru ohraničeného týmito čiarami okolo osi.

Toto je príklad „urob si sám“. Tí, ktorí si želajú, môžu tiež nájsť oblasť postavy „zvyčajným“ spôsobom, čím dokončí test podľa bodu 1). Ale ak, opakujem, otočíte plochú postavu okolo osi, tak dostanete úplne iné telo otáčania s iným objemom, mimochodom, správna odpoveď (aj pre tých, ktorí radi riešia).

Kompletné riešenie dvoch navrhnutých bodov úlohy na konci hodiny.

Jo, a nezabudnite nakloniť hlavu doprava, aby ste pochopili rotačné telá a v rámci integrácie!

Chcel som, už bolo, článok dokončiť, ale dnes priniesli zaujímavý príklad práve na zistenie objemu otáčavého telesa okolo osi y. Čerstvé:

Príklad 7

Vypočítajte objem telesa vzniknutého rotáciou okolo osi obrazca ohraničeného krivkami a. Ľavá nepoužitá vetva paraboly zodpovedá inverznej funkcii - graf funkcie sa nachádza na segmente nad osou;

Je logické predpokladať, že objem rotačného telesa treba hľadať už ako súčet objemov rotačných telies!

Používame vzorec:

V tomto prípade:

odpoveď:

IN problém nájsť oblasť postavyčasto sa používa sumarizácia plôch a sumarizácia objemov telies revolúcie je zrejme zriedkavá, keďže takáto rozmanitosť mi takmer vypadla zo zorného poľa. Napriek tomu je dobré, že sa uvažovaný príklad objavil včas - podarilo sa nám vytiahnuť veľa užitočných vecí.

Úspešná propagácia figúrok!

Objem rotačného telesa možno vypočítať podľa vzorca:

Vo vzorci musí byť pred integrálom číslo. Stalo sa to - všetko, čo sa v živote točí, je spojené s touto konštantou.

Ako nastaviť hranice integrácie "a" a "byť", myslím, je ľahké uhádnuť z dokončeného výkresu.

Funkcia... čo je táto funkcia? Pozrime sa na výkres. Plochý obrazec je ohraničený parabolickým grafom v hornej časti. Toto je funkcia, ktorá je zahrnutá vo vzorci.

V praktických úlohách môže byť plochá postava niekedy umiestnená pod osou. To nič nemení - integrand vo vzorci je odmocnený:, teda integrál je vždy nezáporný , čo je celkom logické.

Vypočítajte objem rotačného telesa pomocou tohto vzorca:

Ako som už poznamenal, integrál sa takmer vždy ukáže ako jednoduchý, hlavnou vecou je byť opatrný.

Odpoveď:

V odpovedi je potrebné uviesť rozmer - kubické jednotky. To znamená, že v našom rotačnom tele je približne 3,35 "kociek". Prečo práve kubický Jednotky? Pretože najuniverzálnejšia formulácia. Môžu tam byť kubické centimetre, môžu tam byť kubické metre, môžu byť kubické kilometre atď., toľko malých zelených mužíkov sa vo vašej fantázii zmestí do lietajúceho taniera.

Príklad 2

Nájdite objem telesa vytvoreného rotáciou okolo osi obrazca ohraničeného priamkami,,

Toto je príklad „urob si sám“. Úplné riešenie a odpoveď na konci hodiny.

Uvažujme o dvoch zložitejších problémoch, s ktorými sa v praxi tiež často stretávame.

Príklad 3

Vypočítajte objem telesa získaného otáčaním okolo osi x úsečky obrazca ohraničeného priamkami ,, a

Riešenie: Nakreslíme na výkres plochý útvar ohraničený čiarami ,,,, pričom nezabúdajme, že rovnica určuje os:

Požadovaná figúrka je vytieňovaná modrou farbou. Keď sa otáča okolo osi, získa sa taká neskutočná šiška so štyrmi rohmi.

Objem rotačného telesa sa vypočíta ako rozdiel v objeme tela.

Najprv sa pozrime na postavu, ktorá je zakrúžkovaná červenou farbou. Keď sa otáča okolo osi, získa sa zrezaný kužeľ. Označte objem tohto zrezaného kužeľa.

Zvážte postavu, ktorá je zakrúžkovaná zelenou farbou. Ak otočíte tento obrazec okolo osi, získate tiež zrezaný kužeľ, len o niečo menší. Jeho objem označme .

A samozrejme, rozdiel v objemoch je presne objemom našej „šišky“.

Na zistenie objemu rotačného telesa používame štandardný vzorec:

1) Číslo zakrúžkované červenou farbou je zhora ohraničené priamkou, preto:

2) Obrázok zakrúžkovaný zelenou farbou je zhora ohraničený priamkou, preto:

3) Objem požadovaného rotačného telesa:

Odpoveď:

Je zvláštne, že v tomto prípade je možné riešenie skontrolovať pomocou školského vzorca na výpočet objemu zrezaného kužeľa.

Samotné rozhodnutie sa často robí kratšie, asi takto:

Teraz si dáme prestávku a povieme si niečo o geometrických ilúziách.

Ľudia majú často ilúzie spojené so zväzkami, čo si v knihe všimol aj Perelman (iný). Zaujímavá geometria. Pozrite sa na plochý obrázok v riešenom probléme - zdá sa, že je malý na plochu a objem rotačného telesa je len niečo málo cez 50 kubických jednotiek, čo sa zdá byť príliš veľké. Mimochodom, priemerný človek za celý život vypije tekutinu s objemom miestnosti 18 metrov štvorcových, čo sa mu naopak zdá príliš malý objem.

Vo všeobecnosti bol vzdelávací systém v ZSSR skutočne najlepší. Tá istá kniha od Perelmana, vydaná už v roku 1950, sa veľmi dobre rozvíja, ako povedal humorista, uvažovaním a učí vás hľadať originálne neštandardné riešenia problémov. Nedávno som si s veľkým záujmom znovu prečítal niektoré kapitoly, odporúčam, je to prístupné aj pre humanistov. Nie, nemusíte sa usmievať, že som navrhol bespontovu zábavu, erudícia a široký rozhľad v komunikácii sú super vec.

Po lyrickej odbočke je vhodné vyriešiť kreatívnu úlohu:

Príklad 4

Vypočítajte objem telesa vytvoreného rotáciou okolo osi rovinného útvaru ohraničeného priamkami,, kde.

Toto je príklad „urob si sám“. Všimnite si, že všetky veci sa dejú v pásme, inými slovami, hotové integračné limity sú skutočne dané. Správne nakreslite grafy goniometrických funkcií, pripomeniem vám materiál lekcie o geometrické transformácie grafov : ak je argument deliteľný dvoma: , potom sa grafy roztiahnu pozdĺž osi dvakrát. Je žiaduce nájsť aspoň 3-4 body podľa trigonometrických tabuliek pre presnejšie dokončenie výkresu. Úplné riešenie a odpoveď na konci hodiny. Mimochodom, úloha sa dá vyriešiť racionálne a nie veľmi racionálne.

Nech je linka obmedzená. rovinný obrazec je daný v polárnom súradnicovom systéme.

Príklad: Vypočítajte obvod: x 2 +y 2 =R 2

Vypočítajte dĺžku 4. časti kruhu umiestnenej v I kvadrante (х≥0, y≥0):

Ak je rovnica krivky uvedená v param-tom tvare:
, funkcie x(t), y(t) sú definované a spojité spolu s ich deriváciami na segmente [α,β]. Derivát, potom vykonanie substitúcie vo vzorci:
a vzhľadom na to

dostaneme
pridať násobiteľ
pod koreňovým znakom a konečne sa dostaneme

Poznámka: Je daná rovinná krivka, môžete zvážiť aj funkciu danú parametrami v priestore, potom sa pridá funkcia z=z(t) a vzorec

Príklad: Vypočítajte dĺžku astroidu danú rovnicou: x=a*cos 3 (t), y=a*sin 3 (t), a>0

Vypočítajte dĺžku 4. časti:

podľa vzorca

Dĺžka oblúka rovinnej krivky daná v polárnom súradnicovom systéme:

Nech je rovnica krivky uvedená v polárnom súradnicovom systéme:
je spojitá funkcia spolu s jej deriváciou na segmente [α,β].

Vzorce pre prechod z polárnych súradníc:

považovať za parametrické:

ϕ - parameter podľa f-le

2

Príklad: Vypočítajte dĺžku krivky:
>0

Z-tion: vypočítajte polovicu obvodu:

Objem tela vypočítaný z plochy prierezu tela.

Nech je dané teleso ohraničené uzavretým povrchom a nech je plocha ktorejkoľvek časti tohto telesa známa rovinou kolmou na os Ox. Táto oblasť bude závisieť od polohy roviny rezu.

nech je celé telo uzavreté medzi 2 rovinami kolmými na os x, ktoré ho pretínajú v bodoch x=a, x=b (a

Na určenie objemu takéhoto telesa ho rozdelíme na vrstvy pomocou sečných rovín kolmých na os Ox a pretínajúcich ju v bodoch. V každom čiastočnom intervale
. Poďme si vybrať

a pre každú hodnotu i=1,….,n zostrojíme valcové teleso, ktorého tvoriaca čiara je rovnobežná s Ox a vodidlom je obrys rezu telesa rovinou x=С i, objem taký elementárny valec so základnou plochou S=C i a výškou ∆х i . Vi =S(Ci)∆xi. Objem všetkých takýchto elementárnych valcov bude
. Limita tohto súčtu, ak existuje a je konečná pri max ∆х  0, sa nazýva objem daného telesa.

. Keďže V n je integrálny súčet pre funkciu S(x) spojitú na segmente, potom zadaná limita existuje (t-ma existencie) a je vyjadrená def. integrálne.

- objem telesa vypočítaný z plochy prierezu.

Objem rotačného telesa:

Nech teleso vznikne rotáciou okolo osi Ox krivočiareho lichobežníka ohraničeného grafom funkcie y=f(x), osou Ox a priamkami x=a, x=b.

Nech je funkcia y=f(x) definovaná a spojitá na úsečke a nezáporná na nej, potom rez tohto telesa rovinou kolmou na Ox je kružnica s polomerom R=y(x)=f(x ). Oblasť kruhu S (x) \u003d Py 2 (x) \u003d P 2. Nahradenie vzorca
získame vzorec na výpočet objemu rotačného telesa okolo osi Ox:

Ak sa však krivočiary lichobežník otáča okolo osi Oy ohraničenej grafom súvislým na funkcii, potom objem takéhoto rotačného telesa:

Rovnaký objem možno vypočítať pomocou vzorca:
. Ak je čiara daná parametrickými rovnicami:

Zmenou premennej dostaneme:

Ak je čiara daná parametrickými rovnicami:

y (a) = c, y (p) = d. Zmenou y = y (t) dostaneme:

Vypočítajte rotačné telesá okolo osi y paraboly, .

2) Vypočítajte V rotačného telesa okolo osi OX krivočiareho lichobežníka ohraničeného priamkou y \u003d 0, oblúkom (so stredom v bode (1;0) a polomerom=1), s .

Povrchová plocha rotačného telesa

Nech daný povrch vznikne rotáciou krivky y=f(x) okolo osi x. Je potrebné určiť S tohto povrchu pri .

Nech je funkcia y \u003d f (x) určitá a spojitá, má nezáporné a nezáporné body vo všetkých bodoch segmentu [a; c]

Nakreslíme akordy, ktorých dĺžky označíme (n-akordy)

podľa Lagrangeovej vety:

Plocha celej opísanej prerušovanej čiary sa bude rovnať

Definícia: limit tohto súčtu, ak je konečný, keď najväčší spoj polyčiary max, sa nazýva plocha uvažovanej rotačnej plochy.

Dá sa dokázať, že stoová hranica súčtu sa rovná hranici integrovaného súčtu pre p-tu

Vzorec pre S povrch rotačného telesa =

S plochy vytvorenej rotáciou oblúka krivky x=g(x) okolo osi Oy pri

Kontinuálne s jeho derivátom

Ak je krivka daná parametricky ur-miX=x(t) ,r= t(t) funkcieX’(t), r’(t), X(t), r(t) sú definované na segmente [a; b], X(a)= a, X(b)= bpotom vykonaním substitučnej zmenyX= X(t)

Ak je krivka daná parametricky, keď sa zmení vzorec, dostaneme:

Ak je rovnica krivky daná v polárnom súradnicovom systéme

Srotačná plocha okolo osi bude rovná

Rovnako ako pri probléme s hľadaním oblasti potrebujete sebavedomé kreslenie - to je takmer najdôležitejšia vec (keďže samotné integrály budú často jednoduché). Pomocou metodických materiálov a Geometrických transformácií grafov si osvojíte kompetentnú a rýchlu techniku ​​grafov. Ale v skutočnosti som opakovane hovoril o dôležitosti kresieb v lekcii.

Vo všeobecnosti existuje veľa zaujímavých aplikácií v integrálnom počte, pomocou určitého integrálu môžete vypočítať plochu obrázku, objem rotačného telesa, dĺžku oblúka, povrchovú plochu rotácia a oveľa viac. Takže to bude zábava, buďte optimistickí!

Predstavte si nejakú plochú postavu v rovine súradníc. Zastúpený? ... Zaujímalo by ma, kto čo prezentoval ... =))) Jej areál sme už našli. Okrem toho sa však toto číslo môže tiež otáčať a otáčať dvoma spôsobmi:

- okolo osi x;
- okolo osi y.

V tomto článku sa budú diskutovať o oboch prípadoch. Zaujímavý je najmä druhý spôsob otáčania, ktorý spôsobuje najväčšie ťažkosti, no v skutočnosti je riešenie takmer rovnaké ako pri bežnejšom otáčaní okolo osi x. Ako bonus sa vrátim k problém nájsť oblasť postavy, a povie vám, ako nájsť oblasť druhým spôsobom - pozdĺž osi. Ani nie tak bonus, ako materiál dobre zapadá do témy.

Začnime s najobľúbenejším typom rotácie.

plochá postava okolo osi

Príklad 1

Vypočítajte objem telesa získaného otáčaním obrazca ohraničeného priamkami okolo osi.

Riešenie: Rovnako ako v oblasti problému, riešenie začína kresbou plochej postavy. To znamená, že na rovine je potrebné postaviť obrazec ohraničený čiarami , , pričom netreba zabúdať, že rovnica definuje os . Ako urobiť kresbu racionálnejšie a rýchlejšie, nájdete na stránkach Grafy a vlastnosti elementárnych funkcií A Určitý integrál. Ako vypočítať plochu obrázku. Toto je čínska pripomienka a v tomto bode nekončím.

Nákres je tu celkom jednoduchý:

Požadovaná plochá figúrka je vytieňovaná modrou a práve táto figúrka sa otáča okolo osi.V dôsledku rotácie sa získa taký mierne vajcovitý lietajúci tanier, ktorý je symetrický okolo osi. V skutočnosti má telo matematický názov, ale je príliš lenivé špecifikovať niečo v referenčnej knihe, takže ideme ďalej.

Ako vypočítať objem rotačného telesa?

Objem rotačného telesa možno vypočítať podľa vzorca:

Vo vzorci musí byť pred integrálom číslo. Stalo sa to - všetko, čo sa v živote točí, je spojené s touto konštantou.

Ako nastaviť hranice integrácie "a" a "byť", myslím, je ľahké uhádnuť z dokončeného výkresu.

Funkcia... čo je táto funkcia? Pozrime sa na výkres. Plochý obrazec je zhora ohraničený grafom paraboly. Toto je funkcia, ktorá je zahrnutá vo vzorci.

V praktických úlohách môže byť plochá postava niekedy umiestnená pod osou. To nič nemení - integrand vo vzorci je odmocnený: , teda integrál je vždy nezáporný, čo je celkom logické.

Vypočítajte objem rotačného telesa pomocou tohto vzorca:

Ako som už poznamenal, integrál sa takmer vždy ukáže ako jednoduchý, hlavnou vecou je byť opatrný.

Odpoveď:

V odpovedi je potrebné uviesť rozmer - kubické jednotky. To znamená, že v našom rotačnom tele je približne 3,35 "kociek". Prečo práve kubický Jednotky? Pretože najuniverzálnejšia formulácia. Môžu tam byť kubické centimetre, môžu tam byť kubické metre, môžu byť kubické kilometre atď., toľko malých zelených mužíkov sa vo vašej fantázii zmestí do lietajúceho taniera.

Príklad 2

Nájdite objem telesa vytvoreného rotáciou okolo osi obrazca ohraničeného priamkami , ,

Toto je príklad „urob si sám“. Úplné riešenie a odpoveď na konci hodiny.

Uvažujme o dvoch zložitejších problémoch, s ktorými sa v praxi tiež často stretávame.

Príklad 3

Vypočítajte objem telesa získaného rotáciou okolo osi x úsečky obrazca ohraničeného priamkami , , a

Riešenie: Nakreslite na výkres plochý obrazec ohraničený čiarami , , , , pričom nezabudnite, že rovnica definuje os:

Požadovaná figúrka je vytieňovaná modrou farbou. Keď sa otáča okolo osi, získa sa taká neskutočná šiška so štyrmi rohmi.

Objem rotačného telesa sa vypočíta ako rozdiel v objeme tela.

Najprv sa pozrime na postavu, ktorá je zakrúžkovaná červenou farbou. Keď sa otáča okolo osi, získa sa zrezaný kužeľ. Označme objem tohto zrezaného kužeľa ako .

Zvážte postavu, ktorá je zakrúžkovaná zelenou farbou. Ak otočíte tento obrazec okolo osi, získate tiež zrezaný kužeľ, len o niečo menší. Jeho objem označme .

A samozrejme, rozdiel v objemoch je presne objemom našej „šišky“.

Na zistenie objemu rotačného telesa používame štandardný vzorec:

1) Číslo zakrúžkované červenou farbou je zhora ohraničené priamkou, preto:

2) Obrázok zakrúžkovaný zelenou farbou je zhora ohraničený priamkou, preto:

3) Objem požadovaného rotačného telesa:

Odpoveď:

Je zvláštne, že v tomto prípade je možné riešenie skontrolovať pomocou školského vzorca na výpočet objemu zrezaného kužeľa.

Samotné rozhodnutie sa často robí kratšie, asi takto:

Teraz si dáme prestávku a povieme si niečo o geometrických ilúziách.

Ľudia majú často ilúzie spojené so zväzkami, čo si v knihe všimol aj Perelman (iný). Zaujímavá geometria. Pozrite sa na plochý obrázok v riešenom probléme - zdá sa, že je malý na plochu a objem rotačného telesa je len niečo málo cez 50 kubických jednotiek, čo sa zdá byť príliš veľké. Mimochodom, priemerný človek za celý život vypije tekutinu s objemom miestnosti 18 metrov štvorcových, čo sa mu naopak zdá príliš malý objem.

Vo všeobecnosti bol vzdelávací systém v ZSSR skutočne najlepší. Tá istá kniha od Perelmana, vydaná už v roku 1950, sa veľmi dobre rozvíja, ako povedal humorista, uvažovaním a učí vás hľadať originálne neštandardné riešenia problémov. Nedávno som si s veľkým záujmom znovu prečítal niektoré kapitoly, odporúčam, je to prístupné aj pre humanistov. Nie, nemusíte sa usmievať, že som navrhol bespontovu zábavu, erudícia a široký rozhľad v komunikácii sú super vec.

Po lyrickej odbočke je vhodné vyriešiť kreatívnu úlohu:

Príklad 4

Vypočítajte objem telesa vytvoreného rotáciou okolo osi plochého útvaru ohraničeného priamkami , , kde .

Toto je príklad „urob si sám“. Všimnite si, že všetky veci sa dejú v pásme, inými slovami, hotové integračné limity sú skutočne dané. Správne nakreslite grafy goniometrických funkcií, pripomeniem vám materiál lekcie o geometrické transformácie grafov: ak je argument deliteľný dvoma: , potom sa grafy roztiahnu pozdĺž osi dvakrát. Je žiaduce nájsť aspoň 3-4 body podľa trigonometrických tabuliek pre presnejšie dokončenie výkresu. Úplné riešenie a odpoveď na konci hodiny. Mimochodom, úloha sa dá vyriešiť racionálne a nie veľmi racionálne.

Výpočet objemu telesa vzniknutého rotáciou
plochá postava okolo osi

Druhý odsek bude ešte zaujímavejší ako prvý. Úloha vypočítať objem rotačného telesa okolo osi y je tiež pomerne častým návštevníkom testov. Priebežne sa bude brať do úvahy problém nájsť oblasť postavy druhý spôsob - integrácia pozdĺž osi, to vám umožní nielen zlepšiť svoje zručnosti, ale tiež vás naučí, ako nájsť najziskovejšie riešenie. Má to aj praktický význam! Ako s úsmevom spomínala moja učiteľka metód vyučovania matematiky, mnohí absolventi jej ďakovali slovami: „Váš predmet nám veľmi pomohol, teraz sme efektívni manažéri a svojich zamestnancov riadime optimálne.“ Využívajúc túto príležitosť, vyjadrujem jej tiež veľkú vďaku, najmä preto, že získané vedomosti využívam na zamýšľaný účel =).

Odporúčam prečítať každému, aj úplným tupcom. Okrem toho asimilovaný materiál z druhého odseku bude neoceniteľnou pomocou pri výpočte dvojitých integrálov.

Príklad 5

Daný plochý obrazec ohraničený čiarami , , .

1) Nájdite plochu plochej postavy ohraničenú týmito čiarami.
2) Nájdite objem telesa získaný otočením plochého útvaru ohraničeného týmito čiarami okolo osi.

Pozor! Aj keď si chcete najskôr prečítať len druhý odsek Nevyhnutne prečítajte si prvý!

Riešenie: Úloha pozostáva z dvoch častí. Začnime námestím.

1) Vykonajte kreslenie:

Je ľahké vidieť, že funkcia definuje hornú vetvu paraboly a funkcia definuje dolnú vetvu paraboly. Pred nami je triviálna parabola, ktorá „leží na boku“.

Požadovaná postava, ktorej oblasť sa má nájsť, je zatienená modrou farbou.

Ako nájsť oblasť postavy? Dá sa nájsť „zvyčajným“ spôsobom, o ktorom sa uvažovalo v lekcii. Určitý integrál. Ako vypočítať plochu obrázku. Okrem toho sa oblasť obrázku nachádza ako súčet oblastí:
- na segmente ;
- na segmente.

Preto:

Čo je v tomto prípade zlé na zvyčajnom riešení? Po prvé, existujú dva integrály. Po druhé, odmocniny pod integrálmi a odmocniny v integráloch nie sú darom, navyše sa človek môže zmiasť pri nahrádzaní hraníc integrácie. V skutočnosti integrály, samozrejme, nie sú smrteľné, ale v praxi je všetko oveľa smutnejšie, len som pre túto úlohu vybral „lepšie“ funkcie.

Existuje racionálnejšie riešenie: spočíva v prechode na inverzné funkcie a integrácii pozdĺž osi.

Ako prejsť na inverzné funkcie? Zhruba povedané, musíte vyjadriť "x" cez "y". Najprv sa pozrime na parabolu:

To stačí, ale presvedčte sa, že rovnakú funkciu možno odvodiť aj zo spodnej vetvy:

S priamou čiarou je všetko jednoduchšie:

Teraz sa pozrite na os: pravidelne nakláňajte hlavu doprava o 90 stupňov, ako vysvetľujete (toto nie je vtip!). Obrázok, ktorý potrebujeme, leží na segmente, ktorý je označený červenou bodkovanou čiarou. Navyše, na segmente je priamka umiestnená nad parabolou, čo znamená, že oblasť obrázku by sa mala nájsť pomocou vzorca, ktorý už poznáte: . Čo sa zmenilo vo vzorci? Iba list a nič viac.

! Poznámka: Mali by byť nastavené integračné limity pozdĺž osi striktne zdola nahor!

Nájdenie oblasti:

V segmente teda:

Venujte pozornosť tomu, ako som vykonal integráciu, je to najracionálnejší spôsob a v ďalšom odseku zadania bude jasné prečo.

Pre čitateľov, ktorí pochybujú o správnosti integrácie, nájdem deriváty:

Získa sa pôvodný integrand, čo znamená, že integrácia je vykonaná správne.

Odpoveď:

2) Vypočítajte objem telesa, ktoré vznikne rotáciou tohto obrazca okolo osi.

Výkres prekreslím do trochu iného dizajnu:

Postava vytieňovaná modrou sa teda otáča okolo osi. Výsledkom je „vznášajúci sa motýľ“, ktorý sa otáča okolo svojej osi.

Aby sme našli objem rotačného telesa, budeme integrovať pozdĺž osi. Najprv musíme prejsť k inverzným funkciám. Toto už bolo urobené a podrobne popísané v predchádzajúcom odseku.

Teraz opäť nakloníme hlavu doprava a študujeme našu postavu. Je zrejmé, že objem rotačného telesa by sa mal nájsť ako rozdiel medzi objemami.

Otáčame figúrku zakrúžkovanú červenou farbou okolo osi, výsledkom čoho je zrezaný kužeľ. Označme tento zväzok .

Zeleným zakrúžkovaným obrazcom otáčame okolo osi a označujeme ho cez objem výsledného rotačného telesa.

Objem nášho motýľa sa rovná rozdielu v objemoch.

Na zistenie objemu rotačného telesa používame vzorec:

Ako sa líši od vzorca z predchádzajúceho odseku? Iba v listoch.

A tu je výhoda integrácie, o ktorej som nedávno hovoril, je oveľa ľahšie nájsť než povýšiť integrand na 4. mocninu.

Odpoveď:

Avšak chorľavý motýľ.

Všimnite si, že ak sa rovnaká plochá postava otáča okolo osi, potom sa ukáže úplne iné rotačné telo s iným, prirodzene, objemom.

Príklad 6

Daný plochý obrazec ohraničený čiarami a osou.

1) Prejdite na inverzné funkcie a nájdite oblasť plochej postavy ohraničenú týmito čiarami integráciou cez premennú .
2) Vypočítajte objem telesa získaného otáčaním plochého útvaru ohraničeného týmito čiarami okolo osi.

Toto je príklad „urob si sám“. Tí, ktorí si želajú, môžu tiež nájsť oblasť postavy „zvyčajným“ spôsobom, čím dokončí test podľa bodu 1). Ale ak, opakujem, otočíte plochú postavu okolo osi, tak dostanete úplne iné telo otáčania s iným objemom, mimochodom, správna odpoveď (aj pre tých, ktorí radi riešia).

Kompletné riešenie dvoch navrhnutých bodov úlohy na konci hodiny.

Jo, a nezabudnite nakloniť hlavu doprava, aby ste pochopili rotačné telá a v rámci integrácie!